智能制造系统AGV小车及缓冲区容量仿真优化

    其中，x为制造单元各缓冲区容量，如图1所示的8个缓存；)为ACV最大容量，因为ACV的容量越大，价格越贵，因此只考虑到ACV最大容量为5的情况；(x，y)为系统实际产量， (x，y)为系统预设产量。各加工中心线前毛坯缓存设置应不少于线后零件缓存设置。

    

    上述目标函数是一个非线性的整数规划模型，而且，组合考虑Acv小车及缓冲区容量配置问题具有复杂的随机性，数学上的精确法求解该模型十分困难；同时，目标函数包含多维变量，存在维数灾的问题，也难以采用传统的随机模型(如排队网)描述系统的状态和行为。因此，本文拟采用仿真优化的方法，解决装备制造系统Acv小车及缓冲区容量配置优化问题。

 

    2仿真模型的建立

    

    根据图1所示的制造系统简图，搭建了基于Tec-nomatix Plant Simulation 8.2(eM-Plant)仿真软件的仿真模型，如图2所示。硬件基本配置为双核CPU 2. 0GHz，2 GB内存的硬件环境。根据某装备制造企业的实际情况，给出仿真模型的假设条件如下。
 

 

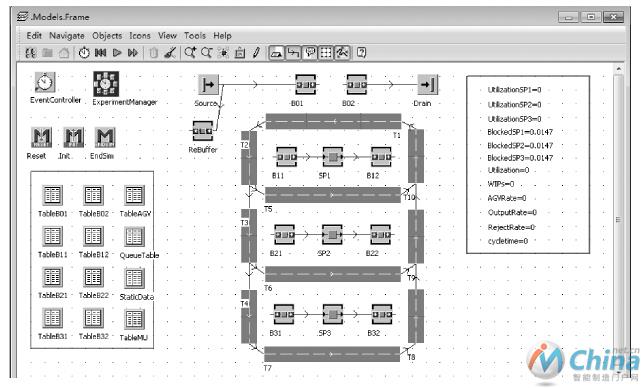
          图2 制造系统仿真模型
 

Fig.2 Manufacturing System Simulation Model

 

    假设1考虑一种工件输入系统，工件到达互相独立，且服从均值为入的泊松分布。

    

    假设2生产环节有3台加工中心，分别只能同时加工一个工件，其加工时间都是互相独立，均服从速率为林，的指数分布(包括装夹时间、准备时间)。

    

    假设3每台加工中心可用性比率为90%，即设备失效率为10%，平均修复时间M}TR (mean time to repair为3h，故障持续时间服从爱尔朗分布。

    

    假设4制造单元服务原则为先到先服务，服从后阻塞机制，各毛坯暂存区和各零件暂存区是有限容量的。

    

    假设5考虑一台ACV小车，最大容量为5，每次运行之间是互相独立，绕3条线运行的平均运送时间不同，且均服从指数分布.

    

    假设6小车配送原则为负荷均衡原则，不考虑小车的装卸时间。

    

    根据以上假设，仿真模型中系统由物流环节和制造单元组成，如图2所示。工件由订单源产生，订单源按照泊松分布平均每小时产生入个任务，只输入一种订单，然后进入毛坯中心库区BO1，由AGV小车运输至其中一个加工中心(SP1，SP2，SP3)前的线前暂缓区(B11，B21，B31)等待加工，完工后的零件将进入加工中心后面的线后成品区(B12， B22，B32)，等待AGV小车将其运回零件中心库B02，然后离开系统。AGV小车配送原则为自动循环运行，出行时AGV小车为线前暂缓区(B11，B21，B31)中最少工件数的暂缓区服务，装载工件时小车按照将毛坯最少的暂存区补满或小车最大装载量原则，回程时小车为零件数最多的暂存区服务，装载零件时按照最大量装载原则。3台加工中心的加工时间都服从指数分布，总的处理速率为林个//h，失效率均为10 % ， M}TR为3 ho AGV小车绕3条线运行的平均运送时间不同，且均服从指数分布。其中图2所示的卜表示一个产生任务的订单源，唇表示一个缓冲区，容量大小可调整，：}.表示一个加工中心，每次只能同时处理一个工件，表示一台AGV小车，承载量与速度可调整。Cycletime  ， OutputRate  ， Utiliza-tion ， AGV Rate ， Rej ectRat。分别代表系统：平均生产周期、产出率、设备利用率、AGV利用率和任务拒绝率。

 

    3仿真优化方法

 

    3.1仿真优化原理

    

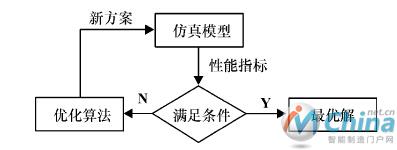
    仿真优化的基本原理，利用仿真模型来替代传统优化模型中的目标函数和约束条件，由优化算法产生一组初始解，将该初始解输入到仿真模型，仿真一段时间后，得到这组解的性能指标，将这组解及其性能指标输入到优化算法中搜索迭代得到一组新解，这组新解比迭代前的解性能更优，再将新解导入到仿真模型，如此反复直到性能指标满足要求，输出最优解，如图3所示。