基于VB的H型钢火焰切割机数控系统开发

3 直线、圆弧轨迹仿真实现的原理

　　3.1 直线轨迹仿真的实现原理

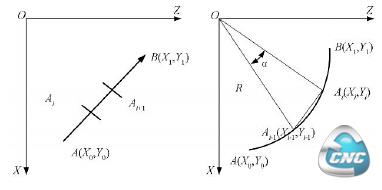
　　如图1所示,令起点A(X₀,Z₀),终点B(X₁,Z₁),则直线方程为:

　　(X₁-X₀)( Y-Z₀) = ( Y₁-Z₀)(X-X0)故tanA= (Z₁-Z₀)/(X₁-X₀)。

　　依据插补原理,将直线AB分解成足够多的有限微小线段AiAi+1,因为Ai在直线AB上,则:Ai(X_i,Z_i),A _i+1(X _i+1,Z _i+1),X _i+1= X_i+△X;Z_i+1= Z_i+△Z,且tanNAiOAi+1=△Z/△X。

　　如果将$X,$Z设置得很小(如0.020mm),直线AB分成足够多的线段AA1,A1A2,A2A3,,,A(N-1)B。设置时钟计时器(Timer)的间隔(Interval)为60ms(为尽量满足坐标显示的实时性,时间间隔不要小于55ms),利用计时器的定时功能,连续画出系列直线AiAi+1。实现直线段AiAi+1的VB程序为:

　　Line(z+Z0,x+X0)-(Z+Z0+△Z,x+X0+△X)

　　其中z,x为时间钟函数的静态变量。由于上一线段的终点就是下一线段的始点,因此这些线段会首尾相连,动态地产生一条直线。同时为使直线能在终点准确到达B点,应使用判断语句(IF语句)。

图1 直线分段               图2 圆弧分段

　　3.2 圆弧轨迹仿真的实现原理

　　圆弧轨迹的生成原理基本与直线的生成原理基本相同。如图2所示,令圆弧起点A(X0, Y0),

　　终点B(X₁, Y₁),圆心在(0,0),半径为R(圆弧方程为:X²+Z²= R²)。依据插补原理,将圆弧AB分成若干份直线段(或圆弧段)AA1,A1A2,A2A3,..A(N-1)B。若用直线段来逼近圆弧,则有:

　　X _i-1 ²+Z _i-1 ²= X_i ²+Z _i ²= R ²
　　X_i= X _i-1+△X
　　Z_i= Z _i-1+△Z

　　由于上述计算很复杂,而且$X和$Z的取法不可能很精确,因此仿真产生的轨迹与真实的圆弧有一定的误差。若用微圆弧段来组成圆弧,依据VB的Circle属性,设定微圆弧对应的圆心角$A,而圆心和半径均不变,这样很容易实现。其过程为:令起点A对应的圆弧起始角为AA,终点B对应的圆弧起始角为AB,微小圆弧段Ai-1Ai的起始和终止圆心角分别为Ai-1,Ai,则:Ai=Ai-1+△A,Ai的坐标为(RcosAi,RsinAi)。

　　其VB的实现程序为:

　　Circle(0,0),R,α,α+△α

　　其中A是系统设置的静态变量。再用IF判断语句实现圆弧准确到达终点。