数控飞锯电气系统的柔性控制数控技术

2 锯切过程的柔性控制

　　2.1 正向起动加速度的控制

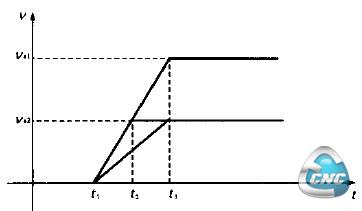
　　图2为正向起动的运行图，我们仅以机组线速度变化为例来加以说明。

图2锯车正向起动运行速度示意图

　　（1）当选择机组线速度v_al= 100m/min=1.667m/S、起动时间△t₁=t₂-t₁ = 0.4S时，加速度a₁= 4.167m/S²，小车起动距离S₁=0.333m，钢管运行长度L₁=0. 6667m。

　　现在定尺长度不变，而机组线速度改变为v_a2= 50m/min=0.833m/S，加速度仍选择a₁=4.167m/S²时，可求出：小车由停止到起动达到同步的加速时间△t₂=t₃-t₁ =v_a2/a₁=0.2S，小车起动距离S₂=v_a2*△t₂/2=0.0833 m，钢管运行长度L₂ = 2*S₂=0.1667 m。

　　上述两种不同线速度情况相比较：△t₂ =0.5△t1；S₂=0.25S1；L₂=0.25L1。

　　比较结果表明：小车达到同步的时间和达到同步的起动距离都成比例下降。但是由于飞锯机械的有效行程的大小是按机组最高线速度和锯切、抬锯时间等因素来设计的，即齿条的长度和飞锯床身的长度是一定的，所以小车同步时间和小车起动距离的减小并无太多实际的好处，带来的结果只是小车在起始位置停留的时间更长一些而已。而此时加速度a=a1，则机械冲击程度和va= va1=1.667m/S时相同，而加速度过大造成的机械损害则是严重的。在机组线速度为100m/min时，因为高速运行，其必须要求加速度a 比较大，这样才能满足数控飞锯正常运行。而在机组线速度为50m/min 时，由于线速度下降一半，则可以将加速度同比例降下来，也可以满足数控飞锯的正常运行

　　（2）当我们选择v_a=v_a2=50m/min=0.833m/S，a=0.5a1=2.083m/S² 时，那么可知此时小车达到同步的时间△t=△t₁=0.4S。由此可计算出：S=v_a*△t/2=0.1667m；L=2*S=0.333m。和va1=100m/min，a₁= 4.167m/S2 相比较，可知：va =0.5v_a1；a= 0.5a₁；△t = △t₁；S=0.5S₁；L=0.5L₁。

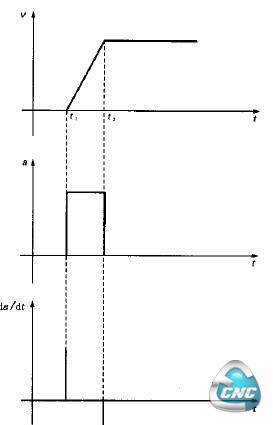
　　由于加速度a下降一半，则正向起动动态转矩可以下降一半，机械冲击明显下降。柔性控制的曲线并不是唯一的，应根据实际可能进行设计选择。我们根据数控飞锯控制系统的闭环传递函数可以求出正向起动的加速度a的表达式，而闭环传递函数中几乎所有参数都可以对加速度a发生影响。这样就应该选择一个或两个最容易来实现控制的参数，根据机组线速度的实际值、定尺长度的设定值来进行自动计算、自动调整。

　　（3）对于正向起动曲线实现柔性控制，我们曾做过二个方案的实验。

　　方案一：选择位置环内一或两个参数来进行加速度控制。这样的结果是位置环的输出曲线的斜率如图2 所示，自动随线速度、定长而改变。

图3锯车理想线性加速示意图 

　　方案二：位置环内参数不改变，只是在位置环输出后面添加一个加速度限制环节。如果v_a = v_a2= 50m/min 时，位置环输出的曲线斜率仍为a=4.167m/S²，而加速度限制环节设定的加速度为a'=2.083 m/ S2 的曲线运行，由于a>a'，将导致位置环输出超调，小车运行速度的最大值将超过v_a = 50 m/ min，从而使同步调整时间加大，当随着（a-a'）/a比值的增加，则位置环输出超调将趋于严重，并可能导致定尺偏差的增大。

　　上述两种方案经实验表明，第一种方案较好，但控制复杂。我们在DF（PLC）-I型控制系统中使用软件方法综合了两种方案，首先在位置环内对正向起动加速度进行自动计算、自动调整，使v_a = v_a1=100m/min 时，位置环输出曲线的斜率为加速度a=a₁=4.167m/S²，当v_a=v_a2=50m/min 时，将输出曲线的斜率自动控制为加速度a=a₂= 2.083m/S²。其次在位置环后面添加了加速度限制环节，选择为a'>a ，即在v_a=v_a1=100 m/ min 时，加速度限制环节自动设定加速度a'> 4.167m/S²。这样，加速度限制环节并不去改变位置环输出曲线的斜率，其作用只是为了保护驱动系统和机械，避免产生非正常的过大的加速度。