五轴联动数控系统RTCP技术的研究与实现

4 RTCP算法的实现

　　基于以上分析，本文从五轴加工中的非线性误差的控制、各轴速度控制及基于参数化配置的运动学模型的建立等方面对RTCP算法进行研究。

　　4.1 非线性误差的控制

　　非线性误差控制是实现RTCP技术的关键问题之一。由于补偿算法与选用的机床类型相关，不失一般性，以下以双转台结构的数控机床为例进行分析。对于其它类型的五轴机床的数学模型与此类似，只是坐标系的选取、旋转轴的代号及旋转变换矩阵有所变化。

　　4.1.1 几何模型的构建

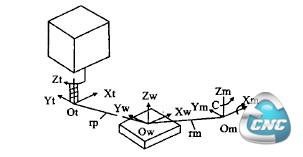
　　为便于机床的运动学描述及简化公式推导，构建机床几何模型，如图2所示。其中坐标系O_wx_wy_wz_w为工件坐标系，

图2坐标系变换关系 

　　基于该坐标系实现工件的程序编制；O_tX_t Y_t Z_t 为刀具坐标系，原点为刀具中心点上；O_mx_m y_m Z_m为与定轴A固联的轴坐标系，原点为旋转中心O_m 其旋转中心O_m在工件坐标系的位置矢量可表示为r_m (x_m ，y_m ，z_m )，刀具中心点在工件坐标系中的位置矢量可表示为r_P(x_P y_Pz_P )，刀具中心点的位置和刀轴矢量分别在刀具坐标系O_tX_t Y_t Z_t  表示为[0 0 0]^T和[0 0 1]^T，机床移动轴相对于机床坐标系的位置矢量为r_s(x_sy_s z_s )。由各坐标系间的几何关系可知，机床加工运动可以由刀具坐标系相对于工件坐标系O_mx_m y_m Z_m 的坐标变换来描述，它可分解为刀具坐标系相对于轴坐标系O_mx_m y_m Z_m 的平动和轴坐标系相对于工件坐标系的转动两部分。

　　4.1.2 基于工件坐标系进行旋转轴角度的线性插补

　　采用线性方式对刀轴矢量进行插补，以对移动轴进行速度规划，旋转轴跟随移动轴的运动方式为例。首先，根据程序段首末点的位置信息及刀轴方向信息，确定各轴运动分量△X，△Y，△Z，△A，△C。

　　计算首末点问的长度：

　　根据以上各轴的运动增量，可以确定刀具中心点的位嚣矢量及刀轴方向矢量。

　　3.1.3 非线性误差的实时补偿

　　根据3.1.2计算的刀具中心点位置矢量及刀轴方向矢量，在每一插补步长内进行非线性误差的补偿。再由机床运动链进行坐标变换，可得：

　　根据上式(2)计算平移变换矩阵r_s然后由r_s确定移动轴在机床坐标系中的坐标值，保证刀心点位于编程轨迹上。

　　4.2基于前瞻算法的速度控制

　　为了提高工件表面的加工质量，本文采用基于刀触点进行加减速规划，但可能造成各轴的速度超出机床的最大加减速能力。为此，本文在加减速控制模块中增加了加工运动误差控制及各轴速度约束，通过对各轴运动速度的调整来保证加工速度的平稳性、使加速度大小不超出机床加减速能力。

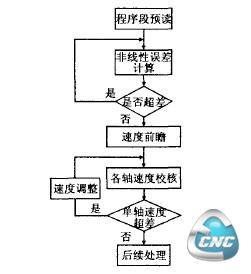
　　速度控制算法的流程图，如图3所示。基于二分法实现轨迹细分，保证各轨迹点问的误差满足加工误差的要求；通过运动学变换实现由工件坐标系中的坐标点到轴坐标系坐标点之间的映射；最后，根据加减速特性，通过各轴速度的前瞻控制算法实现各轨迹点处的最优速度，从而提高加工效率。

图3速度控制流程图