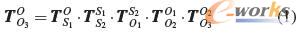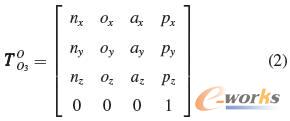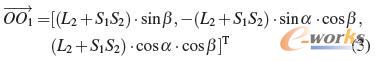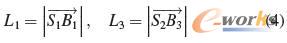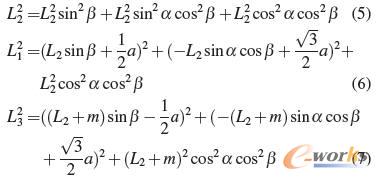一种基于RTLinux的五自由度开放式并联激光加工数控系统

    3.1 建立正反解几何模型

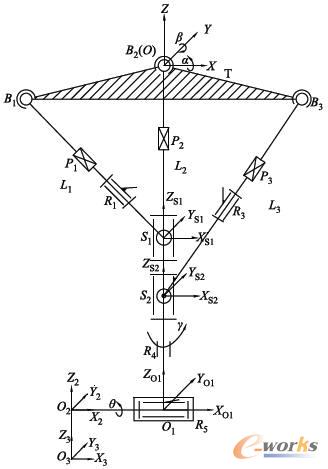
    机器人机构简图如图3所示，在本文所述的机构中，将光轴位姿参数（虚轴坐标）换算到驱动坐标位置（实轴坐标）称为反解运算。

    图3 机器人机构简图

    设定L₂分支中绕X轴旋转虎克铰的旋转角度为α，绕Y轴旋转虎克铰的旋转角度为β，3个分支的杆长分别为L₁、L₂、L₃，串联关节回转转动副和俯仰转动副的转角分别为γ和θ，则由位姿坐标变换可得到：

    已知机器人末端执行器相对于固定参考坐标系O-XYZ的位姿矩阵：

    求解此矩阵方程可得α、β 、γ、θ、L₂。

    根据求解得到的α、β和L₂，将T^O_S2和T^O_O1求解出来。得到S₂和O₁在固定参考坐标系O-XYZ中的坐标，则得到下式：

    在固定平台OB₁B₃中，OB₁B₃为已知三角形，则很容易得到其他两杆长度为：

    正解过程与反解过程正好相反：已知机器人的关节变量L₁、L₂、L₃和γ、θ，求解机器人末端位姿矩阵。

    根据关节变量L₁、L₂和L₃，以及B₁、O、B₃点坐标，列距离方程可以求解到L₂分支绕X轴和绕Y轴的旋转角度α 和β。其求解方程如下：

    根据得到的α和β，将已知的L₂、γ、θ代入到位姿变化矩阵，即可将机器人的末端位姿矩阵求解出来，完成运动学正解。