五自由度自由曲面加工系统及其CAM设计

3 五轴联动机床坐标系统数学模型推导

3.1 五轴联动机床数学模型的推导

    从运动几何学的角度来看，可以将机床看作是关节型机器人，对机床坐标系求解，归根结底属于机器人运动学求反解的问题。也就是在电极丝和加工工件的相对位置关系已知时，求解机床各个轴关节的位移量(包括平动位移和角位移)。根据关节型机器人运动学理沦，在机床每一个关节上建立运动坐标系，随同关节运动，这些运动坐标系是相对坐标系。关节的轴线通常也作为运动坐标系的一个轴，坐标原点一般选在关节轴线上的一个便于识别的特征点上，以方便计算[4|。

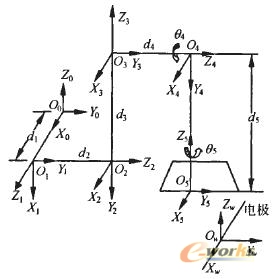
    对图2所示机床建立坐标系统如图4所示。O0是机床的零点坐标系，是固定坐标系。为了以后计算方便，图中在电极丝上建立了电极丝坐标系Oω并且使其坐标轴方向跟05坐标轴初始方向一致，Oω坐标系相对机床来说也是固定不变的，假设Oω坐标系原点在机床零点坐标系O0中的坐标是{△x，△y，△z}。

    从图4可以看出，系统一共有7个变量，由于d4和d5是机床常数，所以需要求解的共有五个位移变量：dl、d2、d3、θ4和θ5，分别是X轴位移、Y轴位移、Z轴位移、B轴摆动角度和C轴转动角度。d1、d2和d3是移动变量，θ4和θ5是转动变量[5]。

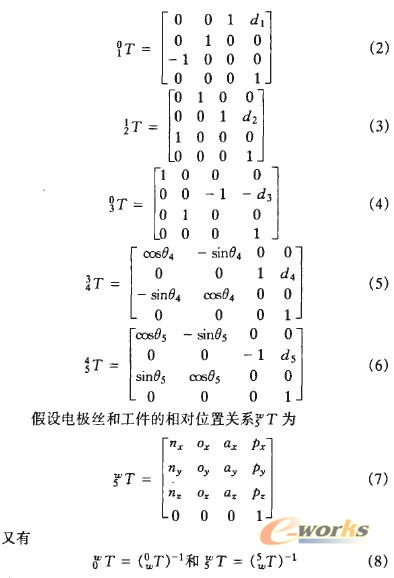
    根据图4首先按照齐次坐标变换方法建立机床各个轴的连杆参数变换矩阵，符号表示Oω坐标系在O0坐标系中的描述，其余类推。

图4 机床坐标系统图

    将式1～8代入下列闭环关系式

    其中，θ4是摆动角度，根据机床实际结构，其取值范围是在(-90°～90°)。当az=0时，θ4处于极限位置一90°(nz<0)或90°(nz>0)。

    θ5是转动角度，存在关系θy=cosθ5和θx=sinθ5。所以，当θy＞0时，θ5处于第一、四象限；当θy<0时，θ5处于第二、三象限；当θy=0时，θ5等于90°的整数倍。

    在上式的推导中，是假设电极丝和加工工件的相对位置为已知量。所以，要想得到最终关系式，必须首先知道。下面以球面为例，说明的求解方法。