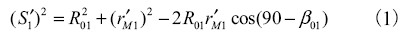螺旋锥齿轮四轴联动数控两刀法加工

　　为了便于描述，四轴数控铣齿机的加工调整参数引用了摇台型机床的概念。在数控铣齿机上，这些加工调整项通过数控程序驱动数控轴进行调整。传统摇台型机床的调整项一经调整，在齿面展成过程中是不能改变的。四轴数控铣齿机的相应调整项是通过数控轴的坐标位置设定实现的，因此在齿面展成时，切削刀盘与工件的相对位置可不断修改。除机床安装角外，其余机床调整基本参数均可以在加工过程中单独改变或几个调整项同时改变。

　　常规的径向刀位改变只能改变齿形的螺旋角，在数控铣齿机上，不但可以很容易地实现常规方法对螺旋角的修正，还可以进行齿长方向的曲率修正。因此，在使用双面刀盘精切小轮凸面时，虽然刀盘半径减小，但可以通过改变径向刀位和角向刀位的方法实现满足设计要求的齿长方向曲率，以达到较好的接触情况。图2 为小轮凸面展成时刀盘与工件的相对位置示意。齿面上的M 点为切齿计算点，当采用原单面精切内刀盘加工时，刀盘中心位于O₀ 点，对应的径向刀位为S₁′角向刀位为q₁′刀盘半径r_M1＝O0,M.数控铣齿机模拟摇台型机床运动时，刀盘中心在平面内的运动轨迹为圆弧。当使用双面精切刀盘加工凸面时，在同一展成位置，刀盘中心位于0O0′点，对应的径向刀位为S₁′，角向刀位为q₁′ ，刀盘半径为r′_M1，且r′_M1＝0 O′_M ，刀盘中心在平面内通过按一定的轨迹运动来进行实现齿长方向的曲率。

　　由于刀盘半径减小，在齿面展成的任一时刻，刀盘中心位置发生改变，但工件的安装位置与运动规律不变。于是，产形轮与工件齿面的啮合位置和产形轮的节锥参数R₀₁、β₀₁都没有改变。

　　轨迹法加工小轮凸面时，径向刀位S₁′和角向刀位q₁′可以按照式(1)进行计算。

3 螺旋锥齿轮两刀法数字化加工模型

　　3.1 坐标系

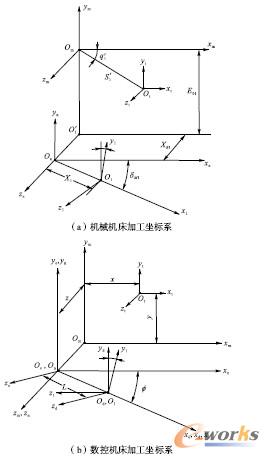
　　图3(a)为传统机械机床坐标系下小轮的加工模型。坐标系Sm＝{Om，xm，ym，zm}为机床坐标系，其中Om为机床中心；坐标系St＝{Ot，xt，yt，zt}为刀盘坐标系，其中zt 轴与刀盘轴线重合；坐标系S1＝{O1，x1，y1，z1}为小轮坐标系，其中x1轴与小轮轴线重合。图3(b)为数控机床坐标系下小轮的加工模型。坐标系Sm与机床固联；坐标系St和S1分别与刀盘、工件(小轮)固联；St和Sn与Sm平行，分别与Y 轴方向滑台、Z 轴方向滑台固联，St原点Ot在Sm中的位置用坐标(x，y，0)表示，描述X 轴和Y 轴的自由度，Sn原点On在Sm中的位置用坐标(0，0，z)表示，描述Z 轴的自由度；因Se 与转台固联，绕yn 轴有一转角φ(即B 轴旋转自由度)；Sd为过渡坐标系，与Se坐标轴平行，原点Od 位置由L(对应机械型中的水平轮位)确定；S1绕x1轴做旋转(即A轴旋转自由度)。

图3 小轮加工坐标系