数控机床加工工艺路线的研究

　　2.2 车圆弧的加工路线分析

　　应用G02（或G03)指令车圆弧，若用一刀就把圆弧加工出来，这样吃刀量太大，容易打刀。所以，实际车圆弧时，需要多刀加工，先将大多余量切除，最后才车得所需圆弧。

　　下面研究分析车圆弧常用加工路线。

图2 圆弧切削路线的形式

　　在图2中，a图表示为同心圆形式，b图表示为等径圆弧（不同圆心）形式，c图表示为三角形形式，d图表示为梯形形式。不同形式的切削路线有不同的特点，了解它们各自的特点，有利于合理地安排其走刀路线。现分析上述几种切削路线：程序段数最少的为同心圆形式及等径圆形式；走刀路线最短的为同心圆形式，其余依次为三角形梯形及等径圆形式；计算和编程最简单的为等径圆形式（可利用程序循环功能），其余依次为同心圆、三角形式和梯形形式：金属切除率最高、切削力分布最合理的为梯形形式；精车余量均匀的为同心圆形式。

图3 阶梯切削路线的车圆弧

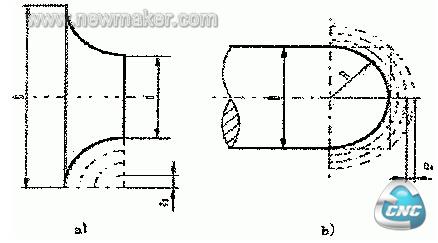
　　图3为车圆弧的阶梯切削路线。即先粗车成阶梯，最后一刀精车出圆弧。此方法在确定了每刀吃刀量ap后，须精确计算出粗车的终刀距S，即求圆弧与直线的交点。此方法刀具切削运动距离较短，但数值计算较繁。

图4 同心圆弧切削路线车圆弧

　　图4为车圆弧的同心圆弧切削路线。即用不同的半径圆来车削，最后将所需圆弧加工出来。此方法在确定了每次吃刀量ap后，对90°圆弧的起点、终点坐标较易确定，数值计算简单，编程方便，常采用。但按图4b加工时，空行程时间较长。

图5 车锥法切削路线车圆弧

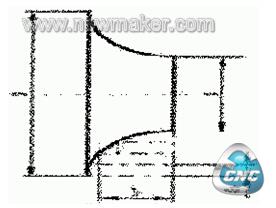
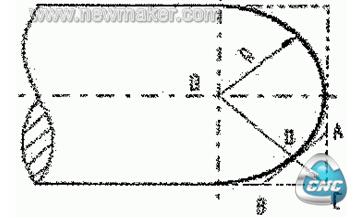
　　图5为车圆弧的车锥法切削路线。即先车一个圆锥，再车圆弧。但要注意，车锥时的起点和终点的确定，若确定不好，则可能损坏圆锥表面，也可能将余量留得过大。确定方法如图5所示，连接OC交圆弧于D，过D点作圆弧的切线AB。

　　由几何关系CD=OC-OD=一日=0.4148，此为车锥时的最大切削余量，即车锥时，加工路线不能超过AB线。由图示关系，可得AC=BC=0.5868，这样可确定出车锥时的起点和终点。当R不太大时，可取AC=BC=0.5R。此方法数值计算较繁，刀具切削路线短。

图6 切削螺纹时引入、引出距离

3、车螺纹时轴向进给距离的分析

　　车螺纹时，刀具沿螺纹方向的进给应与工件主轴旋转保持严格的速比关系。考虑到刀具从停止状态到达指定的进给速度或从指定的进给速度降至零，驱动系统必有一个过渡过程，沿轴向进给的加工路线长度，除保证加工螺纹长度外，还应增加δ1（2mm~5mm）的刀具引入距离和δ2（1mm~2mm）的刀具切出距离，如图6所示。这样来保证切削螺纹时，在升速完成后使刀具接触工件，刀具离开工件后再降速。

4、轮廓铣削加工路线的分析

　　对于连续铣削轮廓，特别是加工圆弧时，要注意安排好刀具的切入、切出，要尽量避免交接处重复加工，否则会出现明显的界限痕迹。用圆弧插补方式铣削外整圆时，要安排刀具从切向进入圆周铣削加工，当整圆加工完毕后，不要在切点处直接退刀，而让刀具多运动一段距离，最好沿切线方向，以免取消刀具补偿时，刀具与工件表面相碰撞，造成工件报废。铣削内圆弧时，也要遵守从切向切入的原则，安排切入、切出过渡圆弧，来提高内孔表面的加工精度和质量。

5、多孔加工路线的分析

　　对于位置精度要求精度较高的孔系加工，特别要注意孔的加工顺序的安排，安排不当时，就有可能将沿坐标轴的反向间隙带入，直接影响位置精度。