五轴加工奇异问题及其处理方法

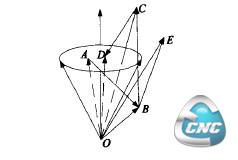
　　如图3所示，从OA到OB经过奇异域，为类型a；OB到OC经过奇异域，为类型C；OC到OD经过奇异域为类型b；OB到OE不经过奇异域。

图3奇异域类型图 

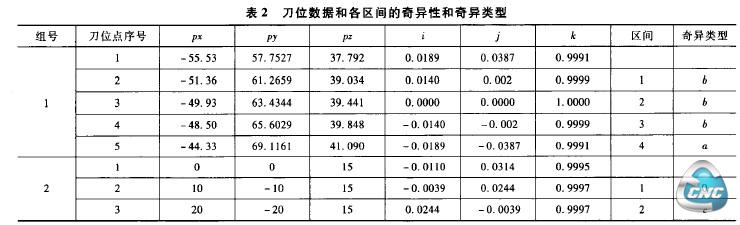
　　根据上面算法，我们可以通过一组数据进行验证算法的有效性。表2为两组刀位点数据和经过本算法所测出的奇异域的位置和类型。由表可知第一组数据区间1～3(第1点到第4点之间)的奇异类型为类型b，而区间4(第4点到第5点之间)的类型为类型a；第二组数据区间1不经过奇异域，区间2类型为类型c。

3 奇异域的处理

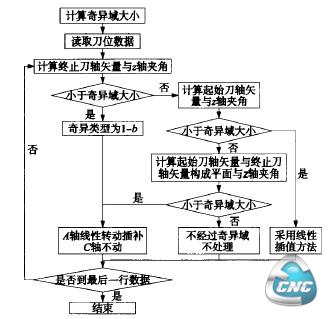
　　当刀具路径通过奇异域时，机床某些轴将剧烈运动．造成过大非线性误差，容易损坏机床，需要进行处理。本文根据所检测出的奇异域类型进行针对性的处理，具体算法：当奇异类型为b和C时，A轴线性转动插值，C轴不动；当奇异类型为a时，AC轴均线性转动插值；当不经过奇异域时，按原来方法处理。具体流程如图4。

图4奇异域处理流程图

4 仿真验证

　　本文对文献中的表1中刀位点(如表3)进行仿真对比，说明本算法的有效性。设定进给速度600mm／min；XYZ轴的最大进给速度为5160ram／min，最大加速度为500mm／s2。插补周期0.002s；C轴最大转速限制为300°每秒；最大角加速度Amax=13.96rad／s2(800”／s2)；最大角加加速度Jmax=7000rad／s3。从而可计算得奇异域大小为dmin=0.0644。RTCP移动坐标轴补偿的机床参数为：A轴旋转中心到C轴旋转中心矢量(0，-0.099，0)；机床零点到工作台安装基点矢量(0．084，0.239，-198.408)；C轴旋转中心到工作零点矢量(-0.084，-0.14，198.408)。

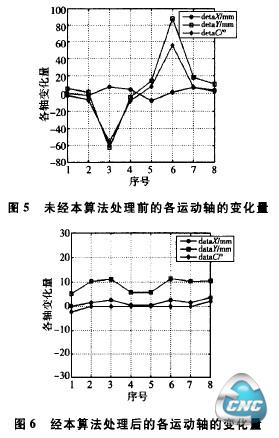
　　图5和图6为表中列出的刀位点未经本算法处理和经过本算法处理描绘出的x、y和C轴坐标的变化曲线。可见，经本算法检测出从第2点到第7点经过奇异域，类型为b，而第7点到第8点的过程也经过奇异域，类型为口。由此可知本算法在求得奇异域的大小范围之后，亦可以如文献中检测出第3和第6区间属于奇异区域。未经过本算法处理之前，奇异位置x轴的最大变化量较小为-8.382mm，而y轴的最大变化量为88.075mm，C轴的最大变化量为55.84。；处理后，三轴的变化量分别减小为3.808mm，11.375mm和2.22°。由此可见经过本算法处理以后运动轴在经过奇异域时速度变化不再那么剧烈。由于z轴和A轴的变化量始终不是很大，故这里不作列出。另外，上述两图中序号分别为区间序号，即表示所取的刀位点中第几对相邻点。

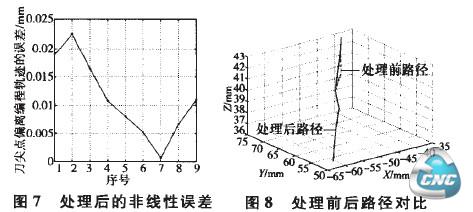
　　图7所示为经过本算法处理的非线性误差，可知经过本算法处理之后的非线性误差降低到0.025mm以下，比文献中处理后的误差小，符合要求。由图8可见在不经本算法处理的情况下，由于机床各轴的最大运动速度所限制，加工路径中出现了尖点的情况，明显偏离理想轨迹，误差较大。而经过本算法处理之后加工路径比较接近理想轨迹。

5 总结

　　本文根据机床的动力学特性求解奇异域大小，并以此作为判断标准，提出一种几何算法，可以根据起始刀轴矢量和终止刀轴矢量，在未经插补的时候，预知五轴加工是否会经过奇异域，并且对加工处于的奇异域状态进行了分类，在后续处理的过程中针对不同的奇异域类型采用不同的插补方法，能够有效的解决奇异问题，避免加工中出现各轴变化量突变和造成机床的损坏，同时也可以减小非线性误差，具有实用性。