结构拓扑优化技术综述

    随后围绕Michell问题解析解的研究工作大致分为两类，Cox和Hemp将Michell桁架的结果应用到弹性结构设计中，而Drucker，Shield和Prager则将Michell桁架理论推广到塑性结构极限设计领域。Cox证明了Michell桁架同时也是一定材料体积用量约束下的最小柔度设计。Hemp对Michell问题进行了更为系统严格的研究，针对Michell准则在不同拉压许用应力约束情况下的缺陷进行了改进。借助Prager-Shield的最优塑性设计理论和库恩一塔克条件，Rozvany也独立地得到了与Hemp相同的改进的Michell准则，并给出了一批典型的Michell桁架解析解。近十几年来，Rozvany，Lewinski，Graczykowski等人继续对Michell问题进行了持续深入的研究并取得了新的进展，他们针对不同载荷形式、不同结构设计域形状。以及不同支承边界形状的情况，精确地得到了一批Michell问题解析解。

    解析求解Michell问题是一件极其困难的工作，至今尚无构造Michell桁架的一般性方法，众多学者长期而艰难的研究也只是获得了若干个Michell桁架的解析解，难以在工程实际问题中广泛应用。1964年，Dorn等人提出基结构方法（groundstructureapproach），将数值方法引入到桁架结构拓扑优化领域，促使桁架结构拓扑优化的研究应用在近几十年里得到较大发展。基于桁架基结构模型，Dobbs和Fetton使用最速下降法求解多工况和应力约束下桁架拓扑优化。Sheu和Schmidt采用分枝定界法求解在应力和位移两类约束下桁架结构在多工况作用下的最优拓扑。

    Ringertz将桁架的横截面积和节点位移同时作为设计变量参与结构拓扑优化设计，采用非线性规划算法和分枝定界法求解。王光远等提出了结构拓扑优化的两相法。Kirsch针对离散结构的拓扑优化问题，提出了一种两阶段算法。1992年，Zhou和Rozvany针对桁架结构考虑节点位移和杆件应力两种约束条件下的最小重量设计问题，发展了一种优化准则类算法（DCOC算法），极大的提高了桁架优化问题的求解规模。近年来，一些适用于并行计算且对优化模型性态要求较低的智能类优化算法开始被应用到桁架结构拓扑优化领域。如遗传算法，粒子群算法，模拟退火算法，蚁群算法以及蜂群算法等。但是，这些算法的求解规模一般来说都不是很大。

    利用数值方法构造Michell桁架是另一类方法。2002年，周克民朝等以纤维增强正交各向异性复合板为材料模型，根据有限元分析结果调整各单元的纤维密度和方向得到了类似Michell桁架的设计。之后，他将此种方法扩展到不同拉压许用应力、多工况以及三维设计域等更为复杂的情况，发展了一种利用有限元技术数值构造Michell桁架的方法。2010年，Sokol利用Mathematica程序语言，开发出一个99行代码的桁架拓扑优化设计程序，为研究者数值地求解Michell问题提供了新的有力工具。借助数值解的预测，最近，Rozvany，Lewinski等人针对更为复杂的一些情况，解析地得到了Michell问题精确解。这种基于数值预测获得Michell桁架解析解的方法，被Rozvany认为是Michell桁架研究领域的一项重大进步。

2.2 连续体结构拓扑优化

    连续体结构拓扑优化最早可以追溯到1981年程耿东和Olhoff的关于实心板最小柔顺性设计的优化工作，他们首次将微结构概念引入优化问题，并以微结构参数（单位长度内肋的个数）对板上加强肋的分布进行描述，得到了允许包含有无限细无限密的肋骨加强的变厚度板的最优设计。这项工作是近代结构拓扑优化研究的先驱性工作，引发了近三十年持续的结构拓扑优化研究。1988年Bendsφe和Kikuchi以设计域内材料分布来描述结构拓扑，提出了结构拓扑优化的均匀化方法，这开创了连续体结构拓扑优化的新局面。目前，连续体结构拓扑优化方面的研究主要集中在：均匀化方法、人工密度法、进化结构优化方法、水平集方法等。

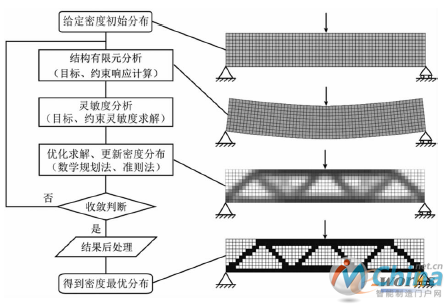
    均匀化方法的基本思想是假定设计域内的每一点，材料具有微结构，以微结构形状和尺寸参数为设计变量，通过优化得到设计域内材料的最优分布。具有微结构的材料的宏观等效性能与微结构之间的关系可以通过均匀化方法获得。对于均匀化方法得到的优化结果，设计域中的任何位置的材料都明确的对应于一种材料微结构形式。人工密度法是以材料的相对密度作为设计变量，通过特定的材料插值模型，比如SIMP或是RAMP，替代均匀化方法来建立材料相对密度和材料性能之间的关系。类似均匀化方法，人工密度法优化结果中的中间密度区域仍然可以视作一种具有特定微结构形式的材料，通过对处于中间密度的材料进行惩罚，使得优化迭代收敛于0/1材料分布。不同于均匀化方法，人工密度法不需要引入真实的材料微结构和附加均匀化求解，程序实现简单，优化效率高，故而得到广泛应用。图4给出了连续体结构拓扑优化的一般流程。

图4 连续体结构拓扑优化一般流程

    受满应力结构设计准则的启发，1993年Xie和Steven提出了进化结构优化方法，其主要思想是按照给定的材料删除准则，迭代地删除无效或是低效的材料以得到最优的结构拓扑。这类方法旨在避免连续体结构拓扑优化方法中过多的数学理论，希望直接利用物理概念和计算机高效的求解能力来进行结构拓扑优化，其难点在于构造合理的准则以确保能够有效地评价材料对目标性能的贡献。2000年Sethian和Wiegann将水平集方法引入结构拓扑优化领域，此后，王煜，Allaire等将灵敏度分析技术和水平集方法结合起来，极大地推动了基于水平集方法的结构拓扑优化技术的发展。

    连续体结构拓扑优化可同时对结构的拓扑、形状和尺寸进行优化，是一种获得创新性结构概念性设计的有效方法。数十年来，连续体结构拓扑优化方法已被广泛应用于多个领域的研究工作和实际工程问题中。主要有：考虑多种约束条件（重量、应力、稳定性、制造性等）下，结构的刚度、强度、动力特性优化设计；柔性机构设计；冲击吸能结构设计；流固耦合、热固耦合结构设计；指定材料性能设计或材料一结构一体化设计以及考虑多工况、多目标的结构拓扑优化设计等。

3 结构拓扑优化问题的求解算法

    结构拓扑优化问题的求解算法主要有优化准则法和数学规划法。当然也有一些学者采用一类智能优化算法（遗传算法、神经网络算法和模拟退化算法等）来求解结构拓扑优化问题，尤其是桁架结构的拓扑优化设计。

    优化准则法是一种显式的设计变量更新算法，其主要思想是基于极值点满足的必要条件，即KKT条件，来推导最优解满足的准则，然后构造合适的迭代格式来更新设计变量，直到收敛。对于较少约束条件下的优化问题，优化准则法具有求解问题规模大，效率高等优点，加之其物理概念直观，易于程序化，已被一些商用软件所采用。但是，对于多约束问题，最优化准则的构造就需要相应地引入很多不同的拉格朗日乘子，而这些拉格朗日乘子的决定非常困难，这样就大大的降低了优化求解的效率。另外，由于KKT条件并非最优解的充分必要条件，因此优化准则法并不能保证一定得到最优解，这都大大限制了优化准则法的适用范围。

    数十年来，数学规划法被广泛应用于结构优化设计中，尤其是对于多工况、多约束条件下的结构拓扑优化问题，具有很好的求解能力，极大的弥补了准则法的不足。从优化求解时是否要求提供梯度信息的角度，数学规划法可分为非梯度类算法和梯度类算法。常用的非梯度类算法主要有一维搜索中的二分法和0.618法、Powell方法、单纯形法和复形法等；梯度类优化算法主要有最速下降法、可行方向法、一维搜索中的牛顿法、序列线性规划、序列二次规划、序列凸规划法、内点法以及移动渐近线法等。

4 结论和展望

    本文分别从桁架和连续体校对对结构拓扑优化的重要理论、关键技术等方面进行了较为详尽的描述，尤其有利于工程技术人员对该研究领域的基本情况进行了解。尽管历经三十多年的研究发展，结构拓扑优化技术已经逐渐被众多工程领域所重视，但是受到其自身先天的分析求解规模过大，优化结果难以识别等困难，使得结构拓扑优化技术的应用更多地体现在构件级、简单工况的层面上。因此，未来结构拓扑优化技术的发展应更加注重优化求解的规模、效率以及在复杂工程结构中的应用。