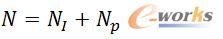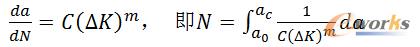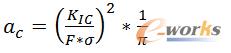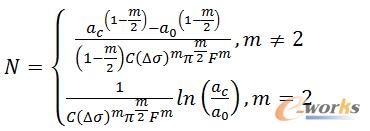基于ANSYS Workbench的裂纹疲劳分析方法的研究

1 引言

    强度、刚度和疲劳寿命是对结构工程和机械工程使用的三个基本要求。疲劳与断裂是引起结构构件和机械零件失效的最主要原因。因此开展结构捕捞研究有着重要意义。在21世纪的今天，人们对传统强度，即静载荷作用、无缺陷材料的强度，这些理论的认识已相当深刻，工程中强度设计的实验经验和积累也十分丰富，对于传统强度的控制能力也大大增加。然而工作周期长，材料本身存在缺陷等各方面因素，使得工程实际都具有复杂性，因此疲劳与断裂的失效在工程供越来越突出。

    疲劳破坏是在足够多次的扰动载荷作用之后，形成裂纹或完全断裂。疲劳破坏是一个损伤累积的发展过程，整个过程包括微裂纹的生成与扩展、宏裂纹的形成与扩展、最后导致材料的断裂破坏。在实际工程中，常常遇到对以产生裂纹构件或存在材料缺陷构件的剩余疲劳寿命的估计问题。

    为了解决对以产生裂纹构件或存在材料缺陷构件的剩余疲劳寿命的估算问题，本文基于有限元分析软件ANSYS Workbench的结果，结合裂纹疲劳强度理论，给出了基于ANSYS Workbench计算结果裂纹疲劳的分析方法。

2 疲劳裂纹扩展寿命理论

    构件的疲劳寿命N可以认为是疲劳裂纹萌生寿命NI与裂纹扩展寿命Np之和，即

公式1 疲劳寿命N

    实践证明，在总的疲劳寿命中，N_p所占的比例高达90%以上，因此断裂扩展速率和寿命这一阶段在构件疲劳寿命中起决定作用。

    由帕里斯（P.C.Paris）半经验定律，得到

公式2 帕里斯半经验定律

    要估算疲劳裂纹扩展寿命，首先必须确定在给定载荷作用下，构件发生断裂时的临界裂纹尺寸a_c。

    依据线弹性断裂判据，对于Ⅰ型裂纹，有

公式3 Ⅰ型裂纹

    计算整理得到疲劳裂纹扩展寿命计算公式如下：

公式4 疲劳裂纹扩展寿命计算公式

3 工程实例

3.1工程模型

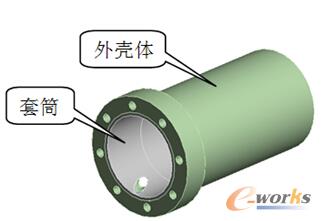
    套筒结构如图1所示。套筒材料为40Cr，其弹性模量E=214GPa，泊松比为v=0.3，抗拉强度为742MPa；外壳体材料为ZL104，其弹性模量E=69GPa，泊松比为v=0.33，抗拉强度为240MPa。

图1 套筒结构图