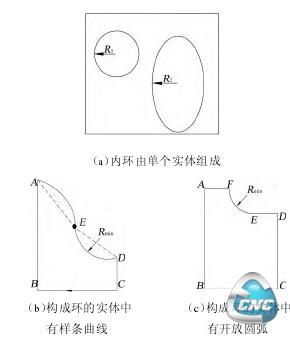
数控加工中半精加工特征的识别及其应用

　　2.3.2.1 凹槽的分类

　　（1）位于环关系树零层的外环之间形成的间隙。最外层环与其他最外层环之间两两求得最小距离，确切地说是间隙值，这是槽间距的第一种类型，如图10所示。

图9 内R角的分类

图10 最外环之间的间隙值

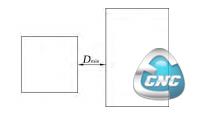
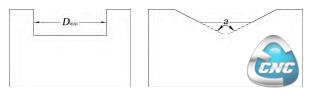
　　（2）内环与其子环之间形成的间隙。在环关系树中若位于奇数层的内环存在子环，则此内环与子环共同构成一段环状间隙，这是槽间距的第二种类型，如图11所示。槽间距值为内环与其子环的最小距离Dmin。

图11 内环与其下一级内嵌外环构成的凹槽

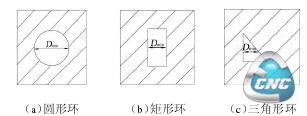
　　（3）环关系树最高层的内环形成的凹槽。位于环关系树最高层的内环在模型中为凹槽或孔洞的截面形状，因为内环的形状变化较多，综合来说有3种典型的情况，如图12所示。对于这3种情况的槽间距取值分别标志在图12中，特别是图12（c）所示的环形状为三角形时，槽间距值取3条边中最短边对应的中位线的长度。

（a）圆形环 （b）矩形环 （c）三角形环
图12 环关系树最高层内环自身形成的凹槽

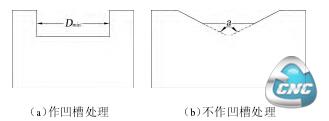
　　（4）外环自身有内凹的部分。外环轮廓有内凹部分时并不是所有情况都算作凹槽，如分别位于内凹轮廓两头的实体所构成的角度大于45°即不能算作凹槽处理，因为这样的内凹部分刀具是否可以深入加工决定于最小内R角半径值不受内凹部分的凹槽间距影响，图13（a）所示轮廓的内凹部分两头实体所构成角度为0，符合对凹槽的定义，槽间距取内凹部分两端点之间的绝对距离。图13（b）中轮廓的内凹部分两头的实体所构成角度a大于45°，不算作凹槽处理。

（a）作凹槽处理 （b）不作凹槽处理
图13 外环自身内凹形成凹槽

　　2.3.2.2 凹槽的识别与槽间距的计算

　　依照凹槽的分类，不同类型的凹槽的识别方法也有差异的，下面针对不同类型的凹槽提出相应的识别方法。

　　（1）针对第一种环关系树零层的外环互相之间形成凹槽的类型，搜索构成轮廓的所有环，记录层值为0的环，两两求最小距离，综合比较这些距离，取最小值作为第一种类型凹槽的最小槽间距值。

　　（2）内环与其子环之间形成的间隙这一类型的凹槽的识别。利用图7所示的环关系树来具体说明，从上至下搜索奇数层的环，搜索到层数为1的环L3和L4，该环关系树除了第一层没有其他奇数层，环L3不存在子环，而环L4存在子环L5，则环L4与L5构成凹槽，求环L4与L5之间的最小距离，即为此类型凹槽的最小槽间距值。

　　（3）环关系树最高层的内环形成的凹槽。这种类型的凹槽识别需要借助环关系树，从下到上搜索奇数层环，并判断位于奇数层的环是否存在子环，若不存在则该环形成第三种类型的凹槽，由于内环的形状变化较多，难以归纳出一个精确确定槽间距的方法，因而作一些近似处理。图12所示为内环的3 种典型形状，图 12（a）内环形状为整圆或椭圆，槽间距为圆的直径或椭圆的短轴长度；图12（b）内环为矩形，槽间距为矩形短边的长度；图12（c）内环为三角形，槽间距为取3条边中最短边对应的中位线的长度。在分析第三种类型凹槽槽间距时将形成凹槽的内环简化成其如图12中的一种，然后求其槽间距值。

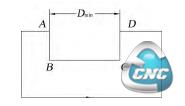
　　（4）外环自身内凹的部分形成的凹槽，这种类型凹槽的识别算法为：图14所示的轮廓方向为逆时针，其中ABCD这段轮廓构成整个环的内凹部分，A、B、C、D 4 个节点的凹凸性分别为凸、凹、凹、凸，由此可以得出规律，轮廓节点的凹凸性按照顺时针或者逆时针顺序排列，若存在凸+n*凹+凸（n≥2）这样的结构，则凸+n*凹+凸（n≥2）构成一个凹槽，识

　　别出组成凹槽的节点后，求2个凸节点之间的绝对距离，工程上将这个距离作为此类凹槽的槽间距，图14所示轮廓的槽间距即为A、D之间的绝对距离Dmin。

图14 外环自身内凹的凹槽的判断