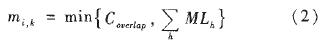柔性制造系统中的结构柔性

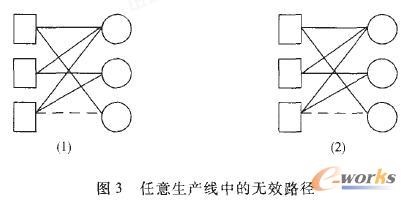
     从产品 1到产品3有三条路径，其中有重叠部分的两条路径如(1)和(2)中粗线部分所示，重叠部分如粗虚线所示。计算这两条路径的最大流量，(1)的最大流量ML1=min(C2,C3),(2)的最大流量ML2=.如何变化，ML2≤ML2都成立。所以在实际计算过程中，(1)的路径不用考虑，我们把这条路径称为无效路径。
    
     对于任意的柔性结构，在计算矩阵中元素时先删除无效路径(这里的删除不是指在结构中删除相应的连线，而是指在计算时不考虑无效路径。因为这里的无效路径是针对某两种产品之间的路径而言，对于其它产品之间，它可能是有效路径)，然后对于有效路径按照下面的方法计算:
    

     Case1 删除无效路径后的结构中，产品两两之间任何路径之间均没有重叠部分.设产品 、到产品 t之间有 H条互不重叠的路径，设MLh为第h条路径的最大流量，MLh就等于第h条路径上生产能力最小的机器对应的能力值 MLh=minCj, Cj表示第j种机器的生产能力，P(h)表示第 h条路径中包含的机器的集合。
    
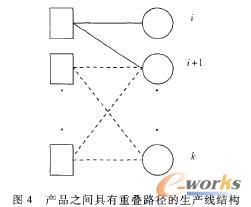
     Case2 删除无效路径的结构中，产品两两之间的路径存在的重叠部分。为了简单起见，设路径只在某两个节点之间重叠，其他部分都是不重叠的(对于存在多处重叠的，只需要进行多次计算)。某特定结构如下(虚线部分所有路径都是不重叠的，图中即为产品i+1到产品k)，设其中重叠部分(粗线所示，图中即为产品 i到i+1)的生产能力为Coverlap。如果重叠部分由多个节点构成，那么Coverlap= minCj，P(overlap)表示在重叠路径上机器的集合。
    
     Proposition.对于上述的结构，如果产品i+1到产品k有H条互不重叠的路径，那么有:
    

     通过计算矩阵的主特征根，我们给出以下的能力扩充的一些规则:
    

     (1)使结构尽可能构成回路(complete the chain)。如果加权短缺不为零并且大于增加完全柔性机器产生的加权短缺，进行下一步;
    
     (2)能力转移矩阵中对角线元素表示能够生产对应产品的最大能力，如果该能力不能满足增加后的需求，所加机器要连接这种产品。如果加权短缺不为零并且大于增加完全柔性机器产生的加权短缺，进行下一步;
    
     (3)连接最有可能需求增加的产品，即需求增加 的概率越大。如果加权短缺不为零并且大于增加完全柔性机器产生的加权短缺，继续进行第3步。
    

     4 结论
    
     当需求发生变化 (某种产 品下一期需求增加)，可以通过增加机器来满足，由于需求增加是随机的，要求增加机器后的生产线结构具有较高的柔性。文中根据生产线的结构特性，给出了的三条增加机器的规则，根据这三条规则，能够快速的得到增加机器的方案。这种方法直接从问题的特性出发，避免了困难的整数规划运算，为这类问题提供了一种新的搜索方法。仿真结果表明，这是一种切实可行的搜索方法，对于大多数问题都能够直接给出最优方案。