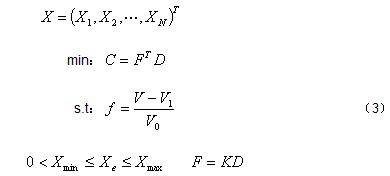多轴越野车辆悬架摆臂结构拓扑优化设计研究

    结构拓扑优化设计是20世纪80年代以来从结构优化研究中派生出来的新分支，已被广泛应用于建筑、航天航空、机械、汽车、海洋工程、生物医学及船舶制造等领域。
   
    拓扑优化又称结构布局优化，是一种根据优化目标、载荷及约束而寻求结构材料最佳分配的优化方法，即将寻求结构的最佳拓扑问题转化为在给定的设计区域内寻求材料的最优分布问题。本文应用Altair公司的OptiStruct软件对某型多轴越野车辆1/2桥悬架的摆臂进行了结构拓扑优化分析，达到了减轻重量、提高刚强度的目的。
   
    1 变密度拓扑优化方法的数学模型
   
    常用的拓扑优化方法有变厚度法、均匀化方法和变密度法等。变密度拓扑优化方法的基本思想是引入一种假想的密度可变材料，将连续结构体离散为有限元模型后，将结构中每个有限单元内的密度指定为相同，以每个单元的密度为设计变量，则有：ρ=X_eρ₀    （1）
   

    式中：X_e为每个单元的相对密度；ρ₀为在设计域里的每个单元的固有密度；ρ为拓扑设计变量。

   

    当X_e=1时，则表示该单元为有材料，保留或增加该单元（实体）；X_e=0时，表示该单元无材料，单元应当删除（孔洞）。拓扑优化时，我们尽量使该材料的密度以0或1分布在设计区域。

    
    拓扑设计变量ρ的0-1特性的不连续性，使得连续变量优化方法中基于导数的有效求解无法进行，因此对其进行连续化。K_e=(X_e)^PK₀   （2）
    
    式中：K_e为单元的刚度；K₀为单元的固有刚度；P为惩罚因子。
   
    若以结构的柔顺度（变形能）最小为目标，考虑材料体积约束（质量约束）和结构的平衡，则拓扑优化的数学模型为：
   

    式中：f为剩余材料百分比；Xmin为单元相对密度的下限；Xmax为单元相对密度的上限；V为结构充满材料的体积；V0为结构设计域的体积；V1为单元密度小于Xmin的那部分材料的体积。
   
    设置Xmax=1，Xmin表示为单元相对密度的下限，其目的是为了使结构的总刚度矩阵不产生奇异，便于求解，同时使被删除的单元能够恢复重新进入计算模型。
   
    2 多轴越野车辆悬架摆臂拓扑优化
   
    2.1 网格摆臂有限元建模及优化设计区域的划分
   
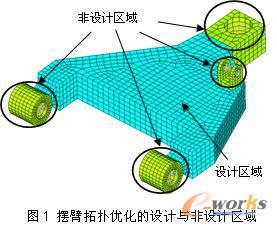
    为了结构拓扑优化分析的需要，填充原始摆臂主体空间并进行网格划分，得到含有5650个单元、7611个节点的摆臂优化分析有限元模型。其中，摆臂与转向节连接球铰处、摆臂与减振器连接支座处及摆臂与车体连接处为非设计区域，其余主体部分为拓扑优化设计区域，如图1所示。
   

    2.2 载荷及位移边界条件
   
    （1）载荷边界条件的确定：考虑以下两种工况下摆臂所受载荷
   
    工况1：摆臂受最大纵向力，在球铰处施加纵向力，FL＝71537N；
   
    工况2：摆臂受最大阻尼力，在减振器支座处施加垂向力，FV=-41123N。
   
    （2）位移边界条件
   
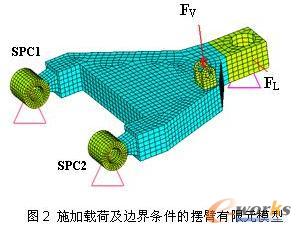
    约束摆臂两销轴处三个平移自由度，约束球铰处垂直方向的平移自由度。施加了载荷及位移边界条件的摆臂有限元模型如图2所示。
   

分页
    2.3 拓扑优化计算及分析结果
   
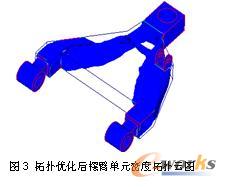
    在完成摆臂优化分析有限元建模的基础上，建立拓扑优化的数学模型。拓扑优化模型包括设计变量、目标函数和约束条件等3个部分。这里以优化设计空间内每个单元的相对密度（Element Density）为设计变量，以最小化综合应变能（Minimize Compliance）为拓扑优化的目标函数，以优化体积比 （Volume Fraction），即优化结构的体积与可设计结构体积的比值作为优化的约束函数。定义优化问题后，系统根据优化问题的设置自动选择最适合的优化算法，经过迭代计算，得到了拓扑优化的分析结果。经过20次迭代运算后，目标函数收敛。取单元密度门槛值为0.2，优化后单元密度拓扑分布云图如图3所示。
   

    2.4 基于拓扑优化结果的摆臂模型重构
   
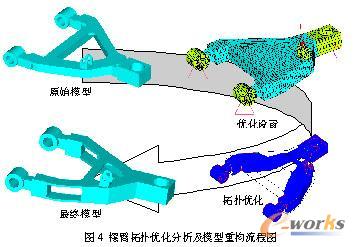
    利用OptiStruct的OSSmooth工具，导出拓扑优化后摆臂的IGES文件，在SolidWorks软件中进行摆臂的几何模型重构，得到最终的优化摆臂模型。摆臂拓扑优化分析及模型重构流程如图4所示。
   

    3 摆臂拓扑优化结果分析
   
    3.1 摆臂结构刚强度分析
   
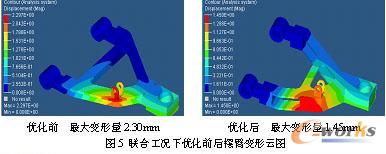
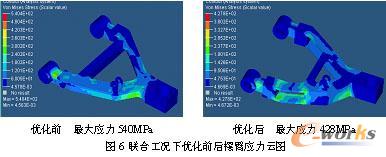
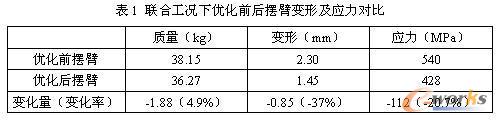
    为了验证优化设计方案结构是否满足设计要求，分别建立结构优化前、后摆臂的有限元模型，计算最大纵向力及最大阻尼力联合工况作用下，摆臂结构的刚强度特性。计算结果对比如表1所示，图5、图6为优化前、后摆臂变形及应力云图。从表中数据对比可以看出，在质量减轻5%的同时，摆臂结构的最大变形量减小了37%，最大应力减小了20%左右。
   

分页
    3.2 摆臂结构模态分析
   
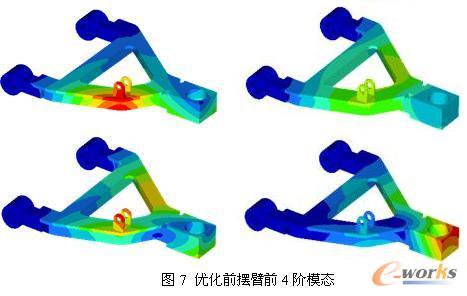
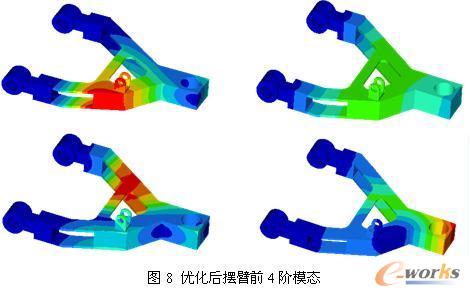
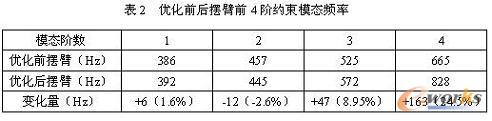
    利用OptiStruct对优化前后摆臂前4阶模态（即进行拓扑优化时的位移约束条件）进行求解，优化前后摆臂前4阶模态频率如表2所示。优化前摆臂结构前4阶模态如图7所示，优化后摆臂结构前4阶模态如图8所示。
   

    3.3 基于整车刚柔耦合动力学模型的摆臂动态强度考核
   
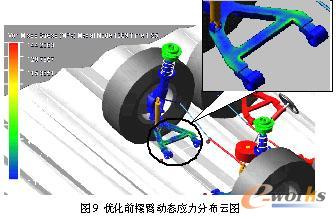
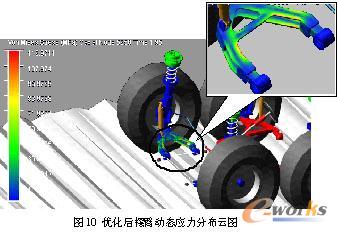
    利用Nastran软件计算出拓扑优化前后摆臂的模态中性文件（MNF），通过ADAMS/Flex接口导入ADAMS/Car中建立摆臂的柔性模型，进而建立多轴越野车辆整车刚柔耦合动力学模型。分别进行车辆以30km/h的速度行驶于F级随机路面工况下的仿真试验，对优化前、后摆臂的动态强度进行考核，如图9、图10所示。拓扑优化前摆臂动态应力最大值为144.2MPa，优化后动态应力最大值为120MPa，减小24.2Mpa，减少幅度达17%。
   

    4 结论
   
    （1）建立了适用于拓扑优化分析的摆臂有限元模型；针对多轴越野车辆悬架摆臂的工作特点，选取了最大纵向力和最大阻尼力工况下的载荷和位移边界条件；设定了拓扑优化的目标函数、设计变量和约束条件；利用OptiStruct软件完成了摆臂的拓扑优化计算；
    （2）基于拓扑优化分析结果，重构了优化后摆臂模型；对比分析了优化前后摆臂的质量、前四阶约束模态、联合工况下的应力和变形，并分别建立了含有柔性摆臂模型的整车刚柔耦合动力学模型，进行了优化前后摆臂的动态强度考核；结果表明，优化后摆臂的质量减少约5%，模态频率有不同程度的提高，联合工况下的应力及变形减小，动态应力最大值减小，动态强度提高；
    （3）通过拓扑优化，在减小摆臂质量的同时提高了摆臂的静、动态刚、强度。本文的研究方法为现有车辆结构零部件的改进设计研究提供了一条参考途径。